09 February 2010

Le sudoku… Un jeu que l’on retrouve dans tous les magazines de nos jours :) . Vous voulez les résoudre sans problèmes sur votre console ? Cet article est pour vous !

Cette méthode n’est pas forcément la plus rapide mais s’il existe une solution, on est sur de la trouver. J’ai choisi de l’implémenter en lua car je l’ai codé pour ma PSP dans mes heures perdues.

Principe

Le principe du backtracking est d’essayer de mettre une valeur dans une case, si cette valeur est possible dans la configuration actuelle du sudoku on continue avec la case suivante. Si la valeur n’est pas correcte on passe à une autre valeur dans cette même case. Si on a essayé toutes les valeurs possibles c’est que l’on s’est trompé avant (ou qu’il n’y a pas de solutions).

On se lance dans le codage

Commençons par définir nos variables :

termine = false – savoir quand la grille à été résolue

-- initialisation de la grille (tableau de 81 cases)
grille = {}
for i=0, 80 do
	grille[i] = 0
end

Ensuite, on va découper le code pour avoir une fonction qui nous renvoie vrai ou faux si la grille est correcte ou pas.

function verifierConstraintes(i) -- int i : indice de la case à tester
	l = math.floor(i / 9)
	c = i % 9
	lb = math.floor(l / 3)
	lr = l % 3
	cb = math.floor(c / 3)
	cr = c % 3
 
	-- verifier la colonne contenant la case i
	for l2=0, 8 do
	    if ( l2 ~= l and grille[l2*9+c] == grille[i] ) then
			return false
		end
	end
 
	-- verifier la ligne contenant la case i 
	for c2=0, 8 do
		if ( c2 ~= c and grille[l*9+c2] == grille[i] ) then
			return false;
		end
	end
 
	-- verifier la region contenant la case i
	for lr2=0, 2 do
		for cr2=0, 2 do
			if ((lr2 ~= lr or cr2 ~= cr) and grille[(lb*3+lr2)*9+(cb*3+cr2)] == grille[i]) then
				return false
			end
		end
	end
 
	-- enfin tout est bon :)
	return true
end

Maintenant, nous attaquons le coeur du programme, la fonction qui est appelée pour résoudre la grille : (j’ai commenté le code pour ne pas avoir à détailler).

function backtrack(i) -- int i : numéro de la case
 
	-- on se contente d'une seule solution donc si la grille est résolue on arrête
	if ( termine ) then
		return
	end
 
	-- grille terminée car on est dans la case 81 (qui n'existe pas ^^)
	if ( i == 81 ) then
		termine = true
		return
	end
 
	-- case contenant déjà une contrainte donc on passe à la case suivante en laissant celle-ci telle qu'elle est
	if ( grille[i] ~= 0 ) then
		backtrack(i+1)
		return
	end
 
	-- la case en cours est donc vide, on essaye successivement les valeurs de 1 à 9
        -- si une valeur est possible on passe à la case suivante en faisant un appel récursif
	for n=1, 9 do
		grille[i] = n
		if ( verifierConstraintes(i) ) then
			backtrack(i+1)
		end
		if ( termine ) then
			return
		end
	end
 
	-- on remet la case à inconnu et on revient en arrière
	grille[i] = 0
end

Voilà, on peut maintenant résoudre n’importe quelle grille avec les codes précédents. Voici tout de même deux captures d’écran et le code complet pour essayer sur votre PSP (ou pas) (interface graphique très primitive ;) ).

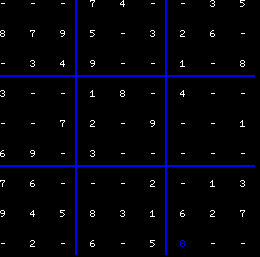La grille avant résolution

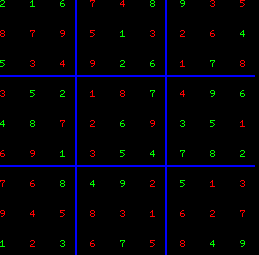La grille après résolution

Code complet

Pour le main, on choisit que : - les flèches déplacent la case pointée - croix ou L décrémente la valeur sur la case pointée - rond ou R incrémente la valeur de la case pointée - carré lance la résolution - triangle vide la grille

Je trouve ce choix assez instinctif :)

--[[ 
Résolveur de sudoku par backtracking
Xavier MICHEL
09/02/2010
--]]
 
 
-- constantes
ESPACEMENT_LIGNE = 30
 
-- variables
rouge = Color.new(255, 0, 0)
vert  = Color.new(0, 255, 0)
bleu  = Color.new(0, 0, 255)
noir  = Color.new(0, 0, 0)
blanc = Color.new(255, 255, 255)
 
cursorx = 0
cursory = 0
 
counter = Timer.new()
counter:start()
 
termine = false
 
-- init grille
grille = {}
for i=0, 80 do
	grille[i] = 0
end
grille2 = {}
for i=0, 80 do
	grille2[i] = 0
end
 
 
function afficherGrille()
	for l=0, 8 do
		for c=0, 8 do
			if ( termine ) then 
				if ( grille2[ l*9 + c ] == 0 ) then 
					screen:print(c*ESPACEMENT_LIGNE, l*ESPACEMENT_LIGNE, grille[ l*9 + c ], vert)
				else 
					screen:print(c*ESPACEMENT_LIGNE, l*ESPACEMENT_LIGNE, grille[ l*9 + c ], rouge)
				end
			else -- non terminée
				if ( cursorx * 9 + cursory == l*9 + c ) then
					if ( grille[ l*9 + c ] == 0 ) then 
						screen:print(c*ESPACEMENT_LIGNE, l*ESPACEMENT_LIGNE, "-", bleu)
					else
						screen:print(c*ESPACEMENT_LIGNE, l*ESPACEMENT_LIGNE, grille[ l*9 + c ], bleu)
					end
				else
					if ( grille[ l*9 + c ] == 0 ) then 
						screen:print(c*ESPACEMENT_LIGNE, l*ESPACEMENT_LIGNE, "-", blanc)
					else
						screen:print(c*ESPACEMENT_LIGNE, l*ESPACEMENT_LIGNE, grille[ l*9 + c ], blanc)
					end
				end
			end
		end
	end
end		
 
 
function verifierConstraintes(i) -- int i : indice de la case à tester
	l = math.floor(i / 9)
	c = i % 9
	lb = math.floor(l / 3)
	lr = l % 3
	cb = math.floor(c / 3)
	cr = c % 3
 
	-- verifier la colonne contenant la case i
	for l2=0, 8 do
	    if ( l2 ~= l and grille[l2*9+c] == grille[i] ) then
			return false
		end
	end
 
	-- verifier la ligne contenant la case i 
	for c2=0, 8 do
		if ( c2 ~= c and grille[l*9+c2] == grille[i] ) then
			return false;
		end
	end
 
	-- verifier la region contenant la case i
	for lr2=0, 2 do
		for cr2=0, 2 do
			if ((lr2 ~= lr or cr2 ~= cr) and grille[(lb*3+lr2)*9+(cb*3+cr2)] == grille[i]) then
				return false
			end
		end
	end
 
	-- enfin tout est bon :)
	return true
end
 
 
function backtrack(i) -- int i : numéro de la case
 
	-- on se contente d'une seule solution
	if ( termine ) then
		return
	end
 
	-- grille terminée
	if ( i == 81 ) then
		termine = true
		return
	end
 
	-- case contenant déjà une contrainte
	if ( grille[i] ~= 0 ) then
		backtrack(i+1)
		return
	end
 
	-- enfin on cherche sur la case vide
	for n=1, 9 do
		grille[i] = n
		if ( verifierConstraintes(i) ) then
			backtrack(i+1)
		end
		if ( termine ) then
			return
		end
	end
 
	-- on remet la case à inconnu et on revient en arrière
	grille[i] = 0
end
 
 
 
-- boucle principale (main)
while true do
	screen:clear()
 
	-- curseur & controles
	pad = Controls.read()
 
	-- déplacement sur la grille
	if pad:down() then
		cursorx = cursorx + 1
		if ( cursorx > 8 ) then 
			cursorx = 0
		end
	end
	if pad:up() then
		cursorx = cursorx - 1
		if ( cursorx < 0 ) then 
			cursorx = 8
		end
	end
	if pad:left() then
		cursory = cursory - 1
		if ( cursory < 0 ) then 
			cursory = 8
		end
	end
	if pad:right() then
		cursory = cursory + 1
		if ( cursory > 8 ) then 
			cursory = 0
		end
	end
 
	-- incrementation nombre pointé
	if pad:circle() or pad:r() then
		grille[ cursorx*9 + cursory] = grille[ cursorx*9 + cursory] + 1
		if ( grille[ cursorx*9 + cursory] > 9 ) then
			grille[ cursorx*9 + cursory] = 0 
		end
	end
 
	-- décrémentation nombre pointé
	if pad:cross() or pad:l() then
		grille[ cursorx*9 + cursory] = grille[ cursorx*9 + cursory] - 1
		if ( grille[ cursorx*9 + cursory] < 0 ) then
			grille[ cursorx*9 + cursory] = 9 
		end
	end
 
	-- lancement résolution
	if pad:square() then
		-- sauvegarde des valeurs précédentes pour la coloration
		for i=0, 80 do
			if ( grille[i] ~= 0 ) then
				grille2[i] = grille[i]
			end
		end
		termine = false
		backtrack(0)
	end
 
	-- vider la grille
	if pad:triangle() then
		for i=0, 80 do
			grille[i] = 0
		end
		for i=0, 80 do
			grille2[i] = 0
		end
		termine = false
	end
 
 
	-- affichage
	afficherGrille()
	screen:fillRect(2*(ESPACEMENT_LIGNE)+ESPACEMENT_LIGNE/2, 0, 2, 255, bleu)
	screen:fillRect(5*(ESPACEMENT_LIGNE)+ESPACEMENT_LIGNE/2, 0, 2, 255, bleu)
	screen:fillRect(0, 2*(ESPACEMENT_LIGNE)+ESPACEMENT_LIGNE/2, 255, 2, bleu)
	screen:fillRect(0, 5*(ESPACEMENT_LIGNE)+ESPACEMENT_LIGNE/2, 255, 2, bleu)
 
	-- boucle anti rep appuis touche
	l=0
	currentTime = counter:time()
	temps = currentTime + 150 
	while l == 0 do
		currentTime = counter:time()
		if currentTime > temps then
			l = 1
		end
	end
 
	screen:flip()
end

algorithme 3

Résoudre Le Sudoku Par Backtracking Ajout d'informations dans la status bar

Principe

On se lance dans le codage

Code complet